Gravitação Universal
Gravitação Universal
A Lei da Gravitação Universal estabelece que, se dois corpos possuem massa, eles sofrem a ação de uma força atrativa proporcional ao produto de suas massas e inversamente proporcional a sua distância.
Peso é uma força exclusivamente atrativa que surge entre dois corpos com massa.
Resumo sobre a Lei da Gravitação Universal
-
Todos os corpos do universo atraem-se mutuamente com uma força proporcional ao produto de suas massas e inversamente proporcional ao quadrado de sua distância;
-
A Lei da Gravitação Universal é definida em termos da Constante de Gravitação Universal, cujo módulo é igual a 6,67408.10-11 N.kg²/m²;
-
A Lei da Gravitação Universal foi descoberta e desenvolvida pelo físico inglês Isaac Newton e foi capaz de prever os raios das órbitas de diversos astros, bem como explicar teoricamente a lei empírica descoberta por Johannes Kepler que relaciona o período orbital ao raio da órbita de dois corpos que se atraem gravitacionalmente.
Introdução à Gravitação Universal
A Lei da Gravitação Universal é uma lei física que foi descoberta pelo físico inglês Isaac Newton. Ela é utilizada para calcular o módulo da atração gravitacional existente entre dois corpos dotados de massa. A força gravitacional é sempre atrativa e age na direção de uma linha imaginária que liga dois corpos. Além disso, em respeito à Terceira Lei de Newton, conhecida como Lei da Ação e Reação, a força de atração é igual para os dois corpos interagentes, independente de suas massas. De acordo com Isaac Newton:
| “Dois corpos atraem-se por uma força que é diretamente proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância que os separa.” |
Por meio da proposição da Lei da Gravitação Universal, foi possível predizer o raio das órbitas planetárias, o período de asteroides, eventos astronômicos como eclipses, determinação da massa e raio de planetas e estrelas etc.
Fórmula da Gravitação Universal
A principal fórmula utilizada na gravitação universal estabelece que o módulo da força gravitacional entre duas massas é proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância entre elas. A expressão utilizada para o cálculo da força gravitacional é esta:
Legenda:
|F| – módulo da força de atração gravitacional (N – Newton)
G – constante de gravitação universal (6,67408.10-11 N.kg²/m²)
M – massa gravitacional ativa (kg – quilogramas)
m – massa gravitacional passiva (kg – quilogramas)
d² – distância entre as massas ao quadrado (m²)
Chamamos de peso
a força de atração gravitacional que uma massa exerce sobre outra. Além
disso, são denominadas de massa gravitacional ativa e passiva a massa
que produz um campo gravitacional ao seu redor e a massa que é atraída por tal campo gravitacional, respectivamente.
A força peso, ou simplesmente o peso de um corpo sujeito a uma gravidade de módulo g, é dada por:
Legenda:
P – módulo da força peso (N – Newton)
m – massa gravitacional passiva (kg – quilogramas)
g – módulo da gravidade local (m/s² – metro por segundo ao quadrado)
Comparando as duas equações acima, podemos perceber que a gravidade de um corpo pode ser calculada pela fórmula a seguir:
A fórmula acima mostra que a gravidade de um planeta, estrela ou qualquer que seja o corpo depende de sua massa (M), da constante de gravitação universal (G) e do inverso do quadrado da distância em que nos encontramos até o centro desse corpo (d), que, no caso de corpos esféricos, é o seu próprio raio.
A Terra, por exemplo, possui massa de 5,972.1024 kg e raio médio de 6371 km (6,371.106 m), logo, podemos calcular o valor médio da gravidade na sua superfície:
Gravitação Universal e a Terceira Lei de Kepler
Um
dos indicadores de sucesso da Lei da Gravitação Universal foi a sua
capacidade de reproduzir a famosa relação matemática descoberta
empiricamente por Johannes Kepler, conhecida como Lei Harmônica:
Para
tanto, basta recordar que a força de atração gravitacional aponta
sempre na direção que liga os dois corpos, tratando-se, portanto, de um
tipo de força central, assim como a força centrípeta, que atua nos corpos em movimento circular. Assim:
Legenda:
v – velocidade de translação do corpo (m/s – metros por segundo)
ω – velocidade angular (rad/s – radianos por segundo)
T – período de translação (s – segundos)
A fórmula indica que a razão do quadrado do período de translação de um corpo em torno de sua massa gravitacional ativa
(por exemplo, a translação da Terra em torno do Sol) pelo cubo do raio
médio da órbita (distância média entre a Terra e Sol, por exemplo) tem
módulo constante, que depende da constante de gravitação universal (G) e
da massa gravitacional ativa M (a massa do Sol, por exemplo).
Constante de gravitação universal
A constante de gravitação universal é uma constante de proporcionalidade de módulo igual a 6,67408.10-11 N.kg²/m², presente
na Lei da Gravitação Universal e usada para igualar a razão do produto
da massa de dois corpos pelo quadrado de sua distância com o módulo da
força de atração entre eles. A constante de gravitação universal é dada,
em unidades do Sistema Internacional de Unidades, em N.m²/kg².
A
constante da gravitação universal foi determinada entre 1797 e 1798
pelo experimento da balança de torção, realizado pelo físico e químico
britânico Henry Cavendish. O experimento tinha como objetivo inicial a determinação da densidade da Terra, mas na época também pôde determinar a constante da gravitação universal com menos de 1% de erro em relação ao valor conhecido atualmente.
Exercícios sobre Gravitação Universal
Questão 1
A
lua é um satélite natural que orbita o planeta Terra pela ação da
grande força gravitacional exercida pela gravidade terrestre. Sendo a
massa da Terra igual a 5,972.1024 kg, a massa da lua 7,36.1022 kg e a distância média entre a Terra e a Lua igual a 384.400 km (3,84.108 m), determine:
Dados: G = 6,67408.10-11 N.m²/kg²
a) a força gravitacional que a Terra exerce sobre a Lua
b) a força gravitacional que a Lua exerce sobre a Terra
c) o módulo da aceleração adquirida pela Lua e pela Terra
Resolução
a) Para calcular a atração gravitacional que a Terra exerce sobre a Lua, usaremos a Lei da Gravitação Universal:
b) De acordo com a Terceira Lei de Newton, a Lei da Ação e Reação, se a Terra exerce uma força de ação sobre a Lua, esta deve exercer uma força atrativa sobre a Terra de mesmo módulo e direção, porém, no sentido oposto, logo, a força que a Lua faz sobre a Terra também é de 20.1019 N.
c)
Se nos lembrarmos da Segunda Lei de Newton, que nos diz que o módulo da
força resultante sobre um corpo é igual ao produto de sua massa pela
sua aceleração, podemos calcular a aceleração adquirida pela Lua e pela
Terra facilmente. Observe:
Os valores de aceleração calculados acima mostram que, apesar de as forças de atração serem iguais para a Terra e para a Lua, a aceleração adquirida por cada uma é diferente. Além disso, fazendo a razão entre os dois valores, vemos que a aceleração que a Lua sofre é cerca de 81 vezes maior que a sofrida pela Terra.


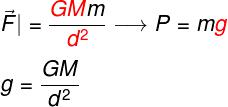

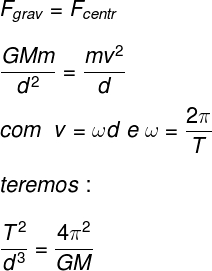

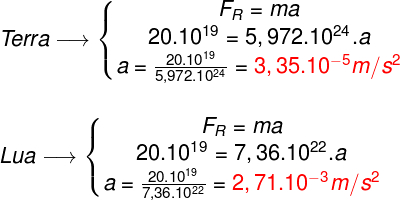


Sem comentários