Movimento uniforme

O movimento uniforme ocorre quando um móvel desloca-se em linha reta e com velocidade constante. No movimento uniforme, o móvel percorre espaços iguais em intervalos de tempo iguais.

Imagine a seguinte situação: um veículo que se move em movimento uniforme, com velocidade de 20 km/h, terá se deslocado de sua posição inicial em 10 km, em um intervalo de tempo de 0,5 h (30 minutos). Em 1h, esse mesmo veículo terá se distanciado de sua posição inicial em 20 km.

Todos os movimentos uniformes devem ocorrer em linha reta, já que nesse tipo de movimento não há aceleração. Entenda: para que um móvel sofra uma alteração em sua direção de deslocamento, é necessário que uma força atue sobre ele, imprimindo-lhe uma aceleração e fazendo com que o móvel ganhe uma nova componente de velocidade.

Não pare agora... Tem mais depois da publicidade ;)

Fórmulas do movimento uniforme

Confira algumas fórmulas utilizadas para descrever o movimento uniforme e entenda o significado de cada uma de suas variáveis:

S — posição final do móvel
S₀ — posição inicial do móvel
v — velocidade do móvel
t — intervalo de tempo

v — velocidade média
ΔS — deslocamento
Δt — intervalo de tempo

 

Referenciais e classificação do movimento

Para definirmos corretamente o movimento de um corpo, é necessário escolher um referencial. Na Física, entendemos que referencial é a posição em que o observador se encontra. A figura abaixo mostra alguns veículos que se movem em diferentes sentidos ao longo da direção horizontal.

O referencial adotado na figura (marcado pelo ponto 0) é onde o observador se encontra. Segundo esse referencial, os carros, à esquerda, encontram-se em posições negativas, enquanto os carros, à direita, encontram-se em posições positivas.

O referencial indica o sentido dos movimentos.

É importante perceber que a escolha de outro referencial implicaria a mudança das posições iniciais de cada veículo e também a classificação dos seus movimentos. A figura abaixo mostra o que o referencial escolhido percebe: para ele, o carro laranja e o carro prata, à esquerda, afastam-se, enquanto o carro prata, à direita, aproxima-se dele.

Dizemos que, quando um móvel aproxima-se do seu referencial, seu movimento é regressivo. Caso o móvel afaste-se do seu referencial, seu movimento é progressivo. Além disso, atribuímos ao movimento progressivo o sinal positivo para a velocidade. Para o movimento regressivo, utilizamos o sinal negativo, indicando que a distância entre o móvel e seu referencial diminui com o tempo.

Velocidade média

A velocidade média de um móvel é dada pela razão do deslocamento (ΔS) no intervalo de tempo em que o movimento ocorreu. O deslocamento (ΔS), por sua vez, é dado pela diferença entre as posições final e inicial do móvel.

v — velocidade média
ΔS — deslocamento
Δt — intervalo de tempo

Na fórmula da velocidade média, chamamos ΔS de deslocamento. O deslocamento de um móvel pode ser facilmente calculado se soubermos de onde ele saiu (S₀ — posição inicial) e onde ele chegou (S_f — posição final) ao término do movimento, que é delimitado por um intervalo de tempo (Δt), calculado pela diferença de tempo entre os instantes final e inicial (Δt = t_f – t₀). Confira essa fórmula, de forma mais detalhada, a seguir:

 

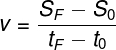
Unidades de medida da velocidade

A unidade de medida da velocidade, de acordo com o Sistema Internacinal (SI), é o metro por segundo (m/s). Porém, existem outras unidades comuns, como o quilômetro por hora (km/h). É fácil convertermos metros por segundo em quilômetros por hora. Para fazê-lo, basta multiplicarmos ou dividirmos o módulo da velocidade pelo fator 3,6, como mostra a figura a seguir:

Exemplos:

72 km/h / 3,6 = 20 m/s

108 km/h /3,6 = 30 m/s

Mapa Mental: Movimento Uniforme

Gráficos do movimento uniforme

Podemos relacionar a posição de um móvel em função do tempo usando os gráficos. Para o movimento uniforme, os gráficos de posição em função do tempo formam retas com inclinação para cima ou para baixo, relacionadas ao movimento progressivo e regressivo, respectivamente. Confira um exemplo de gráfico da posição em função do tempo para o movimento uniforme progressivo:

Na figura abaixo, temos um gráfico que representa a posição em função do tempo para um móvel que executa um movimento uniforme e regressivo (ou retrógrado).

 

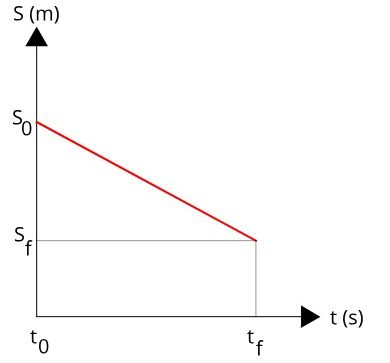
Os gráficos de posição em função do tempo podem ser usados para determinar a velocidade do movimento. Para isso, basta percebermos que a velocidade do móvel é dada por sua tangente, ou seja, a razão entre o cateto oposto (ΔS) e o cateto adjacente à reta (Δt).

Os gráficos de velocidade em função do tempo para o movimento uniforme, por sua vez, são retas paralelas ao eixo horizontal, de módulo negativo ou positivo, de acordo com a sua classificação (progressivo ou regressivo). Por meio do gráfico de velocidade, é possível calcular o deslocamento do móvel, para isso, basta determinarmos o módulo da área abaixo da reta:

No gráfico anterior, a área pintada de azul é numericamente igual à área de um retângulo. Essa área pode ser calculada pela fórmula a seguir:

A — área
b — aresta da base
h — altura

Movimento uniformemente variado

O movimento uniformemente variado é um movimento cuja velocidade aumenta ou diminui de forma constante em relação ao tempo. Esse tipo de movimento não é necessariamente retilíneo e está sujeito a uma aceleração constante. Caso queira saber mais sobre o MUV,

Exercícios sobre movimento uniforme

1) Um móvel parte da posição inicial S₀ = - 15 m e, após 12 segundos, encontra-se na posição S_F = 45 m.

a) Determine a velocidade média desse móvel.

b) Determine a função horária da posição do móvel.

c) Calcule a posição do móvel para os instantes t = 0 s, t = 1 s, t = 2 s, t = 3 s e t = 4 s. Em seguida, construa o gráfico de posição em função do tempo para esse movimento.

d) Classifique o movimento descrito por esse móvel.

Resolução

a) Para calcularmos a velocidade média desse movimento, usaremos a fórmula de velocidade média:

Inserindo os dados fornecidos pelo enunciado do exercício, faremos o seguinte cálculo:

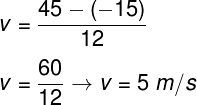
O resultado indica que o móvel desloca-se 5 metros a cada segundo.

b) Para determinar a função horária desse movimento, basta identificarmos a sua posição inicial e velocidade. Em seguida, substituímos esses valores na função horária da posição:

Substituindo os dados do exercício, teremos a seguinte função horária da posição:

c) Vamos calcular a posição do móvel, para cada um dos instantes de tempo citados, usando a sua função horária da posição:

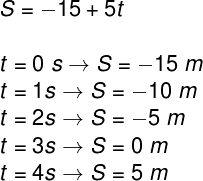
O gráfico desse movimento é mostrado a seguir:

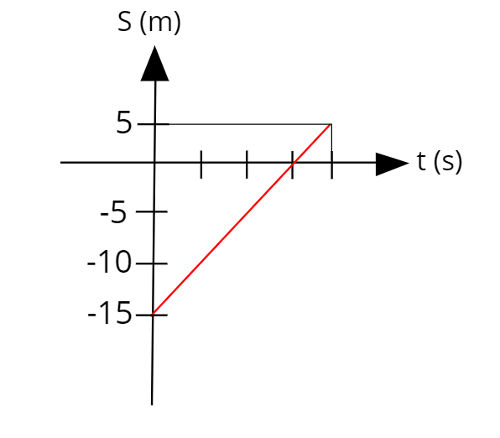
d) Analisando o gráfico, é possível perceber que o móvel aproxima-se do referencial entre os instantes t = 0 s e t = 3 s, a partir de 3 s, o móvel passa a se afastar. Portanto, o movimento é retrógrado entre 0 e 3 s e progressivo de 3 s adiante.